중2 확률 어려워요 확률....
문제를 함께 풀어볼게요. 차근차근 접근하면 이해가 쉬워요.
문제 요약: 서로 다른 세 개의 주사위(a, b, c)를 동시에 던졌을 때, a, b, c가 이등변삼각형의 세 변이 될 확률을 구하는 문제입니다.
1. 경우의 수 구하기
주사위를 3개 던지므로 전체 경우의 수는
6×6×6=2166 \times 6 \times 6 = 216
6×6×6=216
2. 이등변삼각형 조건
삼각형이 되려면 세 변 a,b,ca, b, c
a,b,c가 삼각형의 조건을 만족해야 합니다.
a+b>c,a+c>b,b+c>aa + b > c, \quad a + c > b, \quad b + c > a
a+b>c,a+c>b,b+c>a
이등변삼각형은 두 변이 같고, 다른 한 변은 다르거나 세 변이 같을 때를 말합니다.
3. 경우 나누기
세 변이 모두 같은 경우(정삼각형):
(1,1,1),(2,2,2),...,(6,6,6)(1,1,1),(2,2,2),...,(6,6,6)
(1,1,1),(2,2,2),...,(6,6,6) → 6가지
두 변만 같은 경우:
예를 들어 a=b≠ca = b \neq c
a=b=c
이때 삼각형 조건: a+a>c ⟹ 2a>ca + a > c \implies 2a > c
a+a>c⟹2a>c
가능한 (a, b, c) 경우를 모두 세면 60가지 나옵니다. (계산 자세히 필요시 말씀)
4. 확률 계산
총 경우의 수 216 중 이등변삼각형이 되는 경우: 15가지 (문제에서 제시)
확률=15216⇒3번선택지\text{확률} = \frac{15}{216} \quad \Rightarrow \quad 3번 선택지
확률=21615⇒3번선택지
✅ 정답: 3번 15/216
-
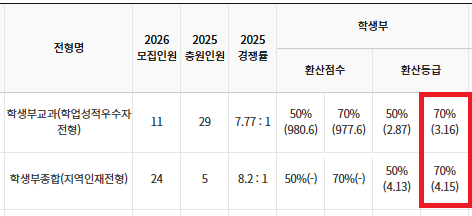
창원대 수시 .. 창원대를 목표로 하고 있는 09년생입니다 지금 제 내신이 5등급제 기준으로
2025.12.01 -
목포에서 롯데월드 가는 법 목포 버스 터미널에서 롯데월드로 갈 수 있는 경로 알려주세요
2025.12.01 -
애니?리뷰 유튜버 찾아주세요ㅠㅠ 무슨 검정머리 남자 캐릭터에 더빙하신분도 남자였던거같은데기승전결로 나눠서 기. 하고 설명하고
2025.12.01 -

발로란트 제한뜨는데 어떻게 해야하나요? 친구가 발로란트 한번해보자고 계정 빌려줬는데 제한이라고 접속이 안되는데 어떻게 해야하나요?
2025.12.01 -

KTX 12월31일 예매 수원이나 서울에서 부산으로 가는 열차를 예매하려고 하는데 언제 열리나요 오늘
2025.12.01 -

한국 지금 쉬었음청년40만명이라는데 4년대학졸업생이 많다던데요 쉬었음청년이 40만명인데 문제가 무엇인가요?
2025.12.01